Multi-fidelity machine learning
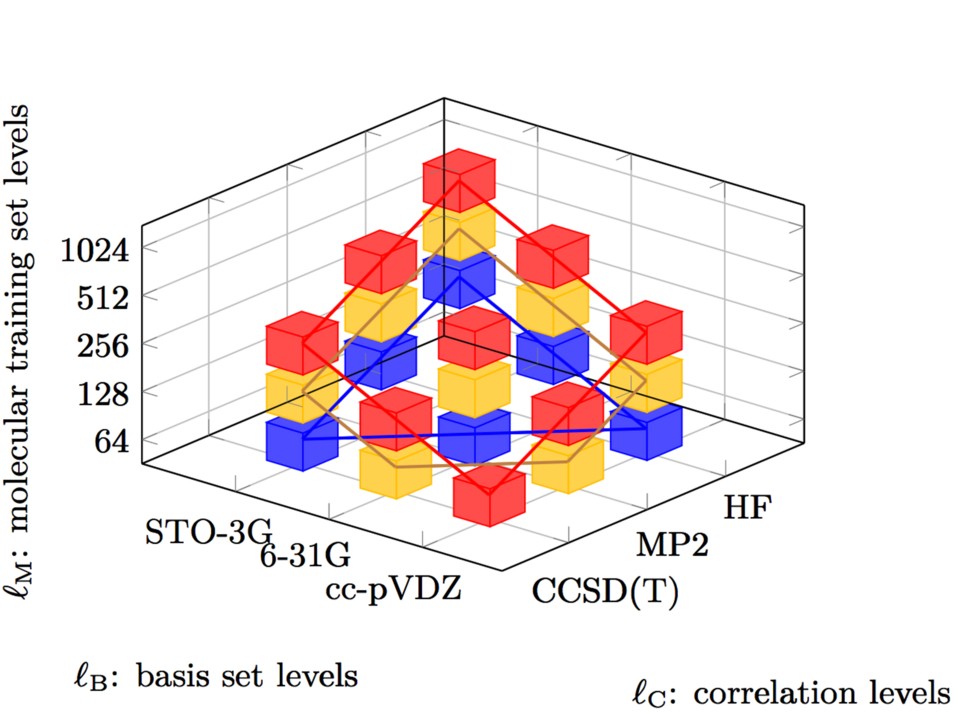
In machine learning, one major focus of the group is currently on multi-fidelity methods, a novel machine learning framework that further includes information on accuracy / fidelities or alternatively cost of the training data in the training process. This approach is of particular interest in real-world applications and simulations in science and engineering, in which such diversity in data is widely available but mostly ignored. The novel multi-fidelity approach [Zas+19] has been introduced based on the sparse grid combination technique [Pfl+14; HZ19b] and is applicable to kernel-based machine learning techniques (kernel ridge regression (KRR), Gaussian process regression, approximation in reproducing kernel Hilbert spaces,…) and (deep) neural networks.
Approximate training
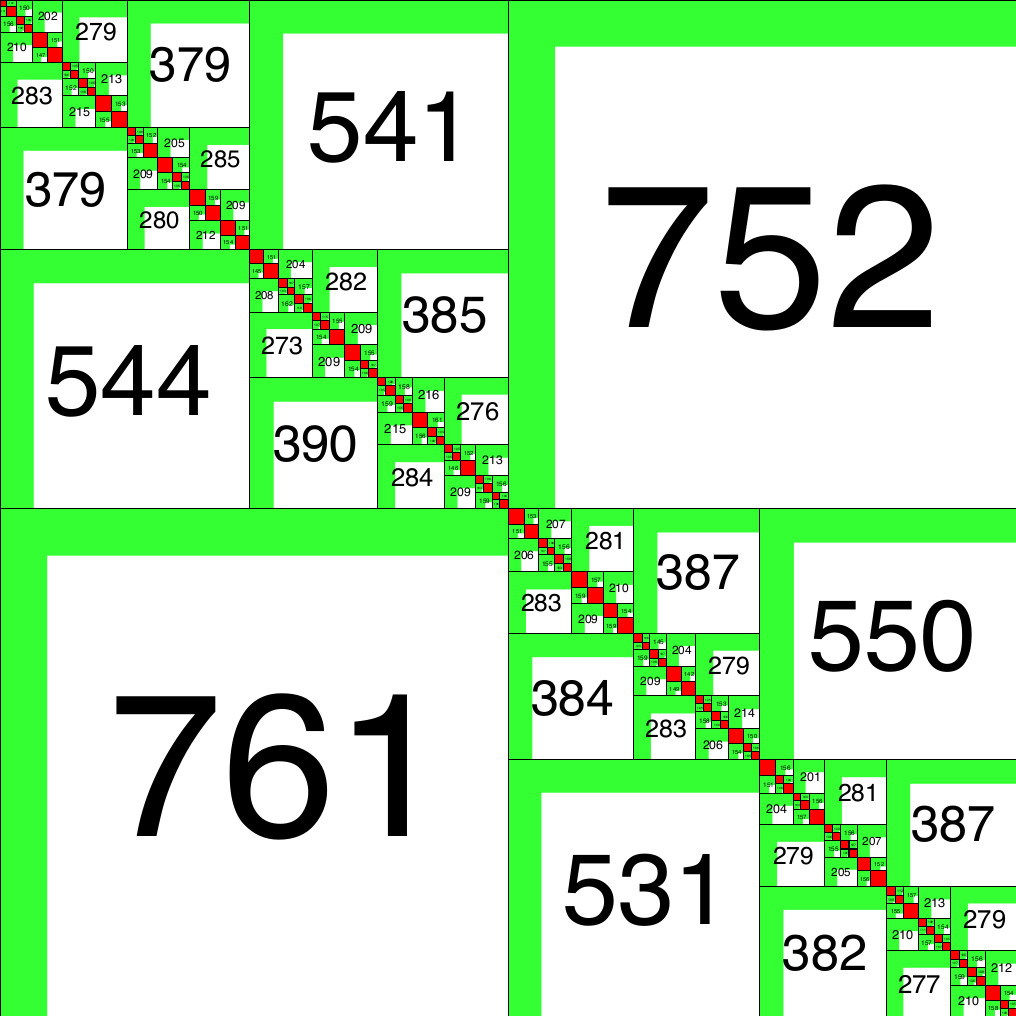
To achieve scalability, approximate training by low-rank approximation techniques based on e.g. hierarchical matrices is used. It should allow to achieve fast and scalable kernel ridge regression training [Zas15; Zas19a; HZ19a]. Here, the the medium-term goal is to construct (parallel) \(O(N log N)\) (instead of \(O(N^3)\)) complexity training methods for kernel-based models, which would boost their use in relation to the currently dominantly used (deep) neural network based methods.
Uncertainty quantification and data assimilation.
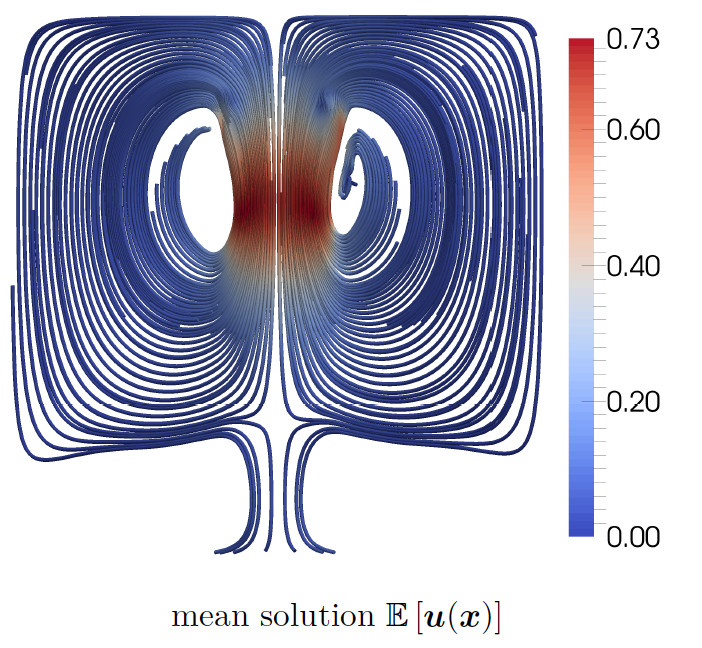
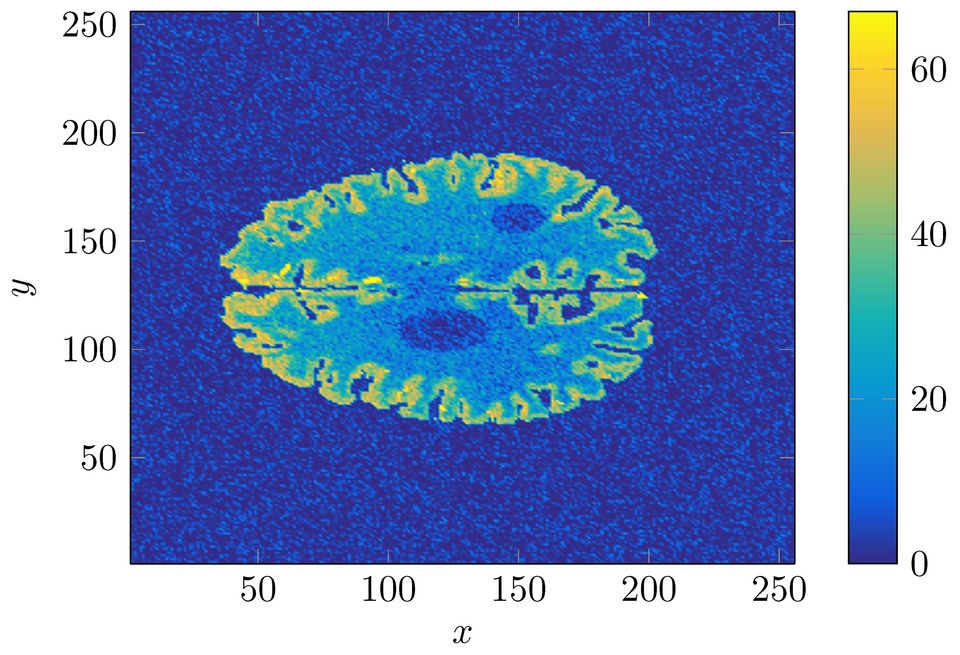
Further work covers methods for uncertainty quantification and data assimilation in the context of mathematical models for e.g. scientific and medical applications. Here, work exists on the fusion of kernel ridge regression and stochastic collocation for stochastic moment analysis of large-scale randomized partial differential equations (PDEs) [Zas15; GRZ19; HJZ20], on modeling deterministic inference problems as Bayesian inference using Kalman filters [Zas19b], and on algebraic construction of “sparse” multilevel methods for stochastic analysis of second moments [Zas16; HZ19b] for elliptic problems with \(O(N^3 \log^p(N))\) complexity instead of \(O(N^6)\) complexity.
Reproducing kernel Hilbert spaces
More generally, basic research with respect to reproducing kernel Hilbert spaces and the related kernel-based machine learning techniques is considered [Zas15; HJZ20].
Related work
- [HJZ20] H. Harbrecht, J.D. Jakeman, and P. Zaspel. “Cholesky-based experimental design for Gaussian process and kernel-based emulation and calibration”. In: Communications in Computational Physics, 2020, accepted.
- [GRZ19] M. Griebel, C. Rieger, and Peter Zaspel. “Kernel-based stochastics collocation for the random two-phase Navier-Stokes equations”. In: International Journal for Uncertainty Quantification, 9(5), 2019, pp. 471–492.
- [HZ19a] H. Harbrecht and P. Zaspel. A scalable H-matrix approach for the solution of boundary integral equations on multi-GPU clusters. Submitted to Computers & Mathematics with Applications, February 2019; available as arXiv Preprint. 2019.
- [HZ19b] H. Harbrecht and P. Zaspel. “On the Algebraic Construction of Sparse Multilevel Approximations of Elliptic Tensor Product Problems”. In: Journal of Scientific Computing, 78(2), 2019, pp. 1272–1290.
- [Zas19a] P. Zaspel. “Algorithmic Patterns for H-Matrices on Many-Core Processors”. In: Journal of Scientific Computing, 78(2), 2019, pp. 1174–1206.
- [Zas19b] P. Zaspel. “Ensemble Kalman filters for reliability estimation in perfusion inference”. In: International Journal for Uncertainty Quantification, 9(1), 2019, pp. 15–32.
- [Zas+19] P. Zaspel et al. “Boosting Quantum Machine Learning Models with a Multilevel Combination Technique: Pople Diagrams Revisited”. In: Journal of Chemical Theory and Computation, 15(3), 2019, pp. 1546–1559.
- [Zas15] P. Zaspel. “Parallel RBF Kernel-Based Stochastic Collocation for Large-Scale Random PDEs”. Dissertation. Institut für Numerische Simulation, Universität Bonn, 2015.
- [Pfl+14] D. Pflüger et al. “EXAHD: An Exa-scalable Two-Level Sparse Grid Approach for Higher-Dimensional Problems in Plasma Physics and Beyond”. In: Euro-Par 2014: Parallel Processing Workshops. Vol. 8806. Lecture Notes in Computer Science. Springer International Publishing, 2014, pp. 565–576.